Algorithms

"Perhaps the most important principle for the good algorithm designer is to refuse to be content."

Next Class

003_1 - 3 - Merge Sort Motivation and Example (9 min)

Course Details

Coursera Onilne Course

Approx. 4 months to complete

Suggested 7 hours/week

Outcomes of the course

• Become a better programmer
• Sharpen your mathematical and analytical skills
• Start "thinking algorithmically"
• Literacy with computer science's "greatest hits"
• Ace your technical interviews

Goal

TIP

To code every Algorithm in Python and in C++

2. How to multiply two integers - A Recursive Algorithm

One way

Write $x=10^{n/2}a + b$ and $y = 10^{n/2} c + d$ where $a, b, c, d$ are $n/2$ digit numbers.

Example: $a=56, b=78, c=12, d=34$

Then,

$x.y = (10^{n/2}a+b)(10^{n/2}c+d)$

$= 10^n ac + 10^{n/2}(ad+bc) + bd \qquad(*)$

Idea:

Recursively compute $ac, ad, bc, bd$, then compute $(*)$ in the obvious way.

Specifically, the relevant products in star, namely AC, AD, BC, and BD all involve smaller numbers than what we started with. Those are all N/2 digit numbers, whereas our original inputs had N digits. So we can legitimately solve those recursively. You can invoke our same algorithm to call to compute those in a recursive way. Now, once we've invoked our multiplication algorithm recursively four times to compute these four relevant products. Now we can just, compute the expression in star in the obvious way. We take AD and BC, we add them together, using the just standard 1st grade iterative addition algorithm. Then we pad both AC and the result of that addition by a bunch of zeroes -- N/2 zeroes or N zeroes as appropriate. Now we have these three constituent terms, and we just add them up again using the grade school algorithm to compute the overall expression.

Karatsuba Multiplication

$x.y = 10^n ac + 10^{n/2}(ad+bc) + bd \qquad(*)$

So here's the trick, and this is really what Gauss figured out over 200 years ago, which is that, it seems there are four products, but fundamentally, in this expression, there's really only three quantities that we care about. There's the AC, the coefficient of this first term, there's AD+BC, the coefficient of this middle term, and there's BD. So we care about AD and BC as quantities individually, only in as much as we care about their sum. We really don't care about them individually. So that motivates the question. Perhaps, we can somehow uncover these three different quantities using only three recursive calls rather than four. In fact we can, and that's Karatsuba multiplication.

1. Recursively compute $ac$
2. Recursively compute $bd$
3. Recursively compute $(a+b)(c+d) = ac+bd+cd+bc$

Gauss's Trick:

And here is Gauss' trick, for observation, which is that the result of the third recursive call minus each of the first two -- what happens. Well the AC is gonna to cancel the AC, the BD is gonna to cancel the BD. And we will be left with AD plus BC, which is exactly that middle co-efficient that we cared about. So, we can indeed compute the sum of AD and BC without separately computing each of them. And that's exactly what we wanted.

$(3) - (1) - (2) = ac+bd+cd+bc - ac - bd = ad+bc$

So, what does this buy us? This gives us another second recursive algorithm for multiplying two integers, that makes use of fewer recursive calls, only three recursive calls, rather than four. And as before, there's a little bit of work to do beyond the recursive calls but not much. You just have to do some padding by zeros and adding up the results.

In particular, does one of these novel recursive approaches do better than the algorithm we learned back in elementary school? The answer to that question is totally non-obvious and it requires non-trivial mathematical analysis to answer. In the upcoming lectures I'll provide you with the tools to not only precisely understand and answer this question but more generally to predict the running times of an entire genre of divide-and-conquer algorithms, like Karatsuba multiplication. So, stay tuned.

Example of Katsubara Algorithm from internet

Karatsuba Multiplication in Python

WARNING

Study and implement this algorithm

❌ Not complete, mark as ✅ when complete

def zeroPad(numberString, zeros, left = True):
    """Return the string with zeros added to the left or right."""
    for i in range(zeros):
        if left:
            numberString = '0' + numberString
        else:
            numberString = numberString + '0'
    return numberString

def karatsubaMultiplication(x ,y):
    """Multiply two integers using Karatsuba's algorithm."""
    #convert to strings for easy access to digits
    x = str(x)
    y = str(y)
    #base case for recursion
    if len(x) == 1 and len(y) == 1:
        return int(x) * int(y)
    if len(x) < len(y):
        x = zeroPad(x, len(y) - len(x))
    elif len(y) < len(x):
        y = zeroPad(y, len(x) - len(y))
    n = len(x)
    j = n//2
    #for odd digit integers
    if (n % 2) != 0:
        j += 1    
    BZeroPadding = n - j
    AZeroPadding = BZeroPadding * 2
    a = int(x[:j])
    b = int(x[j:])
    c = int(y[:j])
    d = int(y[j:])
    #recursively calculate
    ac = karatsubaMultiplication(a, c)
    bd = karatsubaMultiplication(b, d)
    k = karatsubaMultiplication(a + b, c + d)
    A = int(zeroPad(str(ac), AZeroPadding, False))
    B = int(zeroPad(str(k - ac - bd), BZeroPadding, False))
    return A + B + bd

Merge Sort

Why Study Merge Sort

• It's a good introduction to Divide & Conquer paradigm
  • Improves over Selection, Insertion, Bubble sorts
• Motivates guiding principles for algorithm analysis (worst-case and asymptotic analysis)
• Analysis generalizes to "Master Method"

The Sorting Problem

Input: array of n numbers, unsorted.

Output: array of n numbers, sorted in increasing order.

Input	5	4	1	8	7	2	6	3
Output	1	2	3	4	5	6	7	8

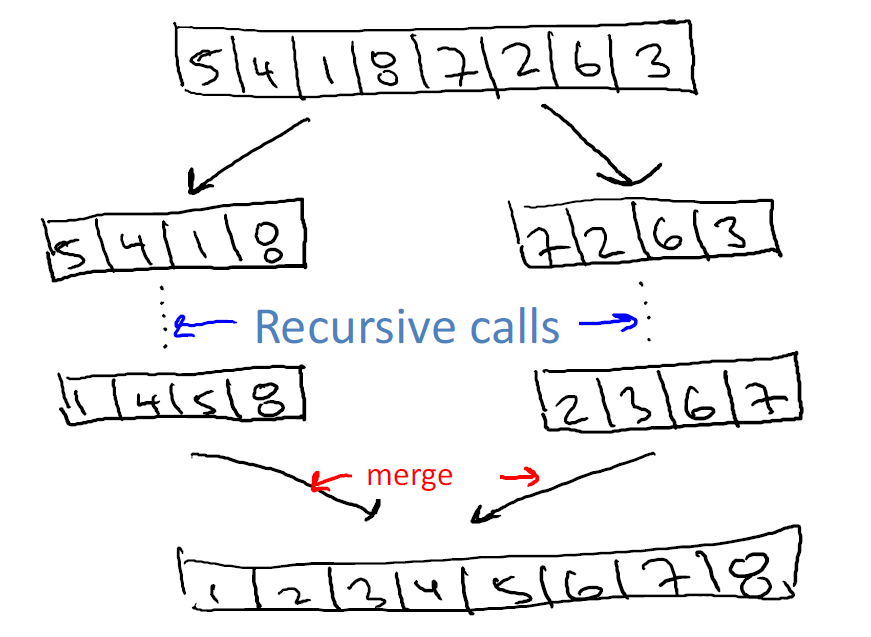
Before I write down any pseudo code for Merge Sort, let me just show you how the algorithm works using a picture, and I think it'll be pretty clear what the code would be, even just given a single example.

So let's go ahead and consider the same unsorted input array that we had on the previous slide.

So the Merge Sort algorithm is a recursive algorithm, and again, that means that a program which calls itself and it calls itself on smaller sub problems of the same form, okay?

So the Merge Sort is its purpose in life is to sort the given input array. So it's going to spawn, or call itself on smaller arrays.

And this is gonna be a canonical Divide-and-Conquer application, where we simply take the input array, we split it in half, we solve the left half recursively, we solve the right half recursively, and then we combine the results.

5	4	1	8	7	2	6	3

So the first recursive call gets the first four elements, the left half of the array, namely 5, 4, 1, 8. And, of course, the other recursive call is gonna get the rest of the elements, 7, 2, 6, 3.

You can imagine these has been copied into new arrays before they're given to the recursive calls.

5	4	1	8		7	2	6	3

Now, by the magic of recursion, or by induction if you like, the recursive calls will do their task.

They will correctly sort each of these arrays of four elements, and we'll get back sorted versions of them.

So from our first recursive call, we receive the output, 1, 4, 5, 8, and from the second recursive call, we received the sorted output, 2, 3, 6, 7.

1	4	5	8		2	3	6	7

So now, all the remains to complete the Merge Sort is to take the two results of our recursive calls, these two sorted elements of length-4, and combine them to produce the final output, namely the sorted array of all eight of the input numbers.

And this is the step which is called Merge.

And hopefully you are already are thinking about how you might actually implement this merge in a computationally efficient way.

In effect, you just walk pointers down each of the two sort of sub-arrays, copying over, populating the output array in the sorted order.

A pseudo code for the merge part would be:

C = output array [length = n]
A = 1st sorted array [n/2]
B = 2nd sorted array [n/2]

i = 1
j = 1

for k = 1 to n
    if A(i) < B(j)
        C(k) = A(i)
        i++
    else [B(j) < A(i)]
        C(k) = B(j)
        j++
end